Scribe post
Learning target: converting fractions to percentages,and converting percents to fractions.
Example: To convert a fraction to a percent you have to create a proportion. If you don't no how to make a porportion check out Robinsong's scribe post. Let's say you have to convert 1/8 into a percent. You would create a porportion which would look like this; 1/8=x/100. Then, you cross multiply: 1*100=100 and x*8=8x. Remember to always put the number before the variable. next, you divide 8x by 8. The solution is x. The key to that is to get the variable all by itself. Following that, you have to divide 100 by 8 because aftter all balance is the key to solving any problem (according to Mr.Tubbs). The solution to this problem is 12.5. so 1/8 equals 12.5 percent. Now let's try converting percemts to fractions. let's say you are trying to make 5 percent a fraction. First, you would make 5 percent into a fraction. This would be 1/20 (I simplified 5/100). Remeber to always put your percentage number over 100 first then simplify.
Check out this link:
http://www.sosmath.com/algebra/fraction/frac7/frac7.html
I found a cool shortcut:
http://video.google.com/videoplay?docid=6213689731166287913&q=converting+fractions+to+percents&hl=en
Scribe post
Learning Target: Developing the area for rectangles, triangles, and parrallelograms.
Formulas: To find the area of a triangle you apply the equation 1/2 (base * height). 
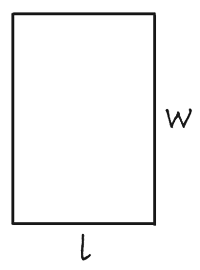
To find the area of a rectangle you apply the
equation length * width.
To find the area for a parrallelogram you apply the equation base * height.

Now let's do some example problems:
If a triangle has the base of 3 inches and the height of 5 inches what is the area?
If you got 7.5 square inches you are correct! You would first multiply the base by the height.
The equation would be 3 times 5 = 15 square inches.
Then divide the product by 2. The equation would be 15/2 = 7.5 square inches.
If a rectangle has a width of 15 inches and the length is 4 inches what is the area?
If you got 60 square inches you are correct! 15 inches * 4 inches= 60 square inches.
If you have a parallelogram that has a base of 11 inches and a height of 8 inches what is the area?
If you got 89 square inches you are wrong 
The correct answer is 88 square inches. The equation for this is 11 inches * 8 inches= 88 square inches.
Check out this video about the area of a rectangle:
http://www.youtube.com/watch?v=ONUhZmBIjPI
Scribe Post #3
Learning Target
Todays learning target was using the prime factorization of composite numbers to find the greatest common factor (GCF), and the least common multiple (LCM).
Example Problem
16 8
/\ /\
8 X 2 4 x 2
/\ /\
4 X 2 2 X 2
/\
2 X 2
2X2X2X2=16 2X2X2 = 8
The GCF (Greatest Common Factor) is eight. This is because each of the numbers has two three times in it ( 2x2x2=8).
The LCM (Least Common Multiple) is sixteen. You find this by making a list of the multiples for each number:
8:8,16,24,32 and
16:16,32,48 then selecting the lowest number in both lists = 16.
Or you could do a multiplication problem . For this problem it would be 2x2x2x2=16. You do this because it contains all the factors required for making both eight and sixteen.
Lesson
You find the GCf by using prime factorization. First you find all the prime factors for each number. Then you determine the product of all the prime factors that occur for both numbers. This product is the GCF.
To find the LCM, you make a list of the first of the first four or five multiples for each number and look for the lowest number that is in both lists. If you don't find one, do the next five multiples and repeat until you find the same number in each list. This is the LCM. Or you can use prime factorization. Once you find the prime factors for both numbers the LCM is the product of all the prime factors of both numbers without any repeted factors.
Check out this link:
http://mathworld.wolfram.com/LeastCommonMultiple.html
SCRIBE POST 1
LEARNING TARGET
Estimate sums and diferences using decimals and fractions.
EXAMPLE PROBLEM
12.34 + 45.78=
12 + 46=58
LESSON
TO ESTIMATE A SUM, YOU ROUND EACH NUMBER TO THE NEAREST WHOLE NUMBER THEN ADD ALL OF THE NUMBERS UP TO GET THE SUM.
TO ESTIMATE A DIFFERENCE, YOU ROUND ALL OF THE NUMBERS TO THE NEAREST WHOLE AND SUBTRACT THEM TO GET THE DIFFERENCE.
EXAMPLE OF DECIMAL
THIS IS PI
Scribe Post